范畴论(Category Theory)是数学的一个分支。研究的不是对象(数值)，而是对象与对象之间的关系。

范畴论的产生可能与人脑本身的结构有关。人脑在解决复杂问题的时候，要将大的问题分解成多个小的问题， 分别解决小的问题，再组合起来。这叫做 compose 。论文 The Magical Number Seven, Plus or Minus Two 指出， 人脑只能保留 $7 \pm 2$ 个片断的信息，因此需要层次化结构的程序。

所有研究 compose 的学科，最底层的逻辑都是 Category Theory 。

Category是什么

Category 中包含两个类别的内容：object 和 morphism。

• object 是 category 中的点
• 一个点向另一个点的变换，称为 morphism (态射)

Category 必须满足以下3点要求(才能被称为一个 Category)：

1. $f: a \rightarrow b$ 和 $g : b \rightarrow c$ 可以组合(compose) 成 $g \circ f$ (读作g after f) ，并且：$g \circ f = a \rightarrow c$
2. 如果存在 $f: a \rightarrow b$ 和 $g : b \rightarrow c$ 和 $h : c \rightarrow d$ ，则 $h \circ ( g \circ f )$ 与 $( h \circ g ) \circ f$ 等价。最终的结果都是 $ a \rightarrow d $。
3. 存在$id_x : x \rightarrow x$，使得 $f \circ id_a = id_b \circ f = f$

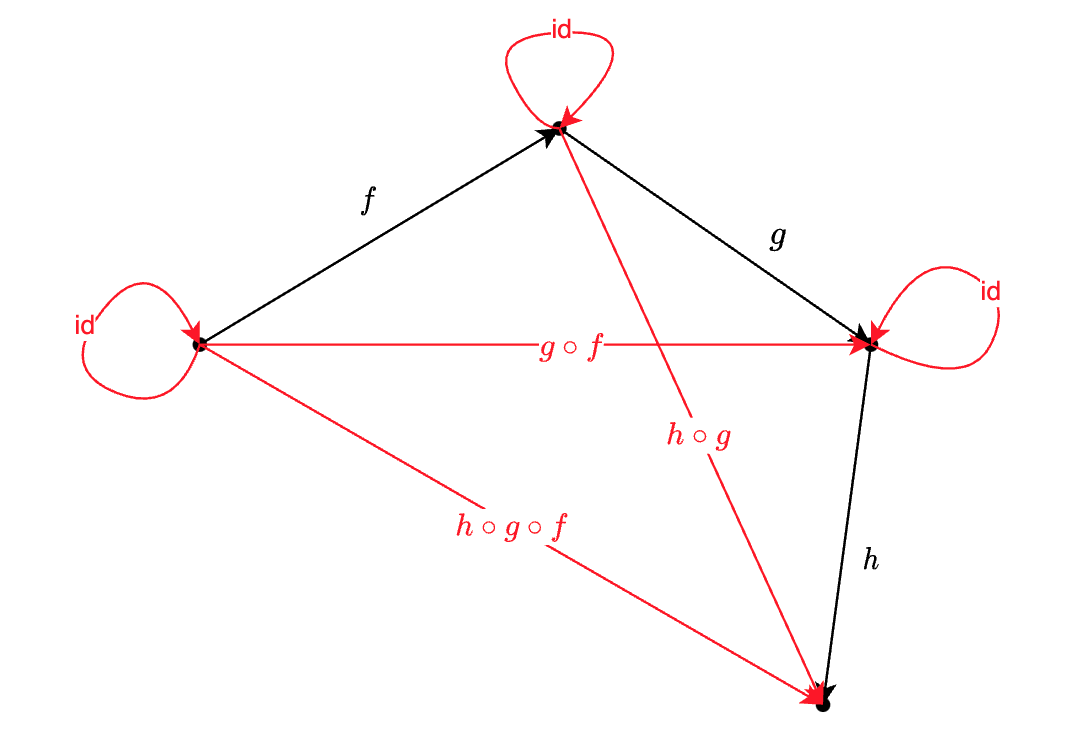
Category 中的 object ，不承载任何信息，承载信息的(我们重点关注的)是点和点之间的关系(morphism)

Category与编程中的概念如何对应

Category 大致可以与编程中的一个类型对应起来。比如如果将整数作为一个 Category，那么object就是所有的整数的值。morphism就是整数与整数之间的变换。

这个阶段，我们关注的变换是单变量的。比如 $1 \rightarrow 2$ 这样的变换，对应的变换的含义其实是 +1。这时 我们可以说，所有的整数，在 +1 这个变换规则下，再用 +0 作为 id 变换，是可以组成一个 Category 的(符合上面所有Category的要求)。

如果一个函数将一个类型转换为另一个类型，比如输入一个整数，返回是否大于0，那就意味着这个函数将一个Category变换到了另一个Category。这就属于Category之间的变换。在这个大的尺度下，如果将Category看成object，将Category之间的变换看成morphism，那就形成了更大的Category。