神经元结构

以下是一个大脑中的神经元的结构：

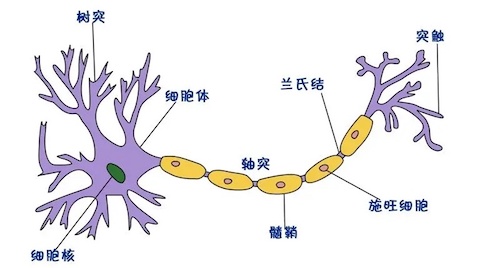
简化来看，大脑的神经元由三部分组成：

1. 树突（输入机制）—— 通过突触接受输入的树状结构。输入可能是来自感觉神经细胞的感觉输入，也可能是来自其他神经细胞的“计算”输入。单个细胞可以有多达10万输入（每个来自不同的细胞）。
2. 细胞体（计算机制）—— 细胞体收集所有树突的输入，并基于这些信号决定是否激活输出（脉冲）。
3. 轴突（输出机制）—— 一旦胞体决定是否激活输出信号（也就是激活细胞），轴突负责传输信号，通过末端的树状结构将信号以脉冲连接传递给下一层神经元的树突。

人类的大脑皮质包含大约140-160亿神经元, 小脑中包含大约550-700亿神经元。

将这个神经元进一步简化成一个函数，是这样：

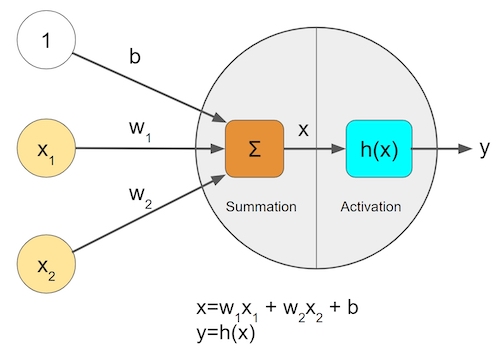
这个函数可以接收n个输入，每个输入对应一个权重，另外有一个激活函数h，用来决定将所有的输入与权重的积求合后的输出。

将很多很多个这样的函数连接起来，就是一个简化的大脑。

可以简单的将人类学习的过程，类比为确定每一个函数的所有权重的过程(训练)。具体每个权重代表什么可能不好解释，但当输入流经一个训练好的网络，最后的输出，就会基于之前学习的权重，产生出一个结果。

神经网络

一个简单的神经网络如下：

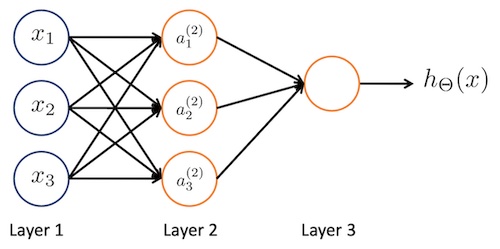
这里面的 $ x_1, x_2, x_3 $ 表示输入，$ a_1^{(2)}, a_2^{(2)}, a_3^{(2)} $表示三个神经元，每一个神经元都是$ x_1, x_2, x_3 $的函数，最终的 $h_{\theta}(x)$表示整个网络的输出。

其中的 $a_1^{(2)}$的函数实际上是：$ g(\theta_{10}^{(1)}x_0 + \theta_{11}^{(1)}x_1 + \theta_{12}^{(1)}x_2 + \theta_{13}^{(1)}x_3) $

神经网络可以从这个基础开始，搭建的越来越复杂。

训练的过程，就是通过事先已知的很多组对应的输入和输出，确定所有$\theta$的过程。

损失函数

在训练的过程中，训练数据集包含输入数据和对应的目标输出数据。而神经网络产生的输出，与训练数据集中的目标输出数据肯定是不一样的，这时候，需要一个函数来描述两者的差距，这个函数就是损失函数。

训练过程的目标是最小化损失函数，以获得最佳的模型参数。

反向传播

一个神经网络搭建好之后，在训练之前，其中所有的权重都是未知的。这个权重的数量可能很大，确定这些变量的值的过程，会使用一个反向传播算法。

反向传播算法（BP 算法）主要由两个阶段组成：激励传播与权重更新。

第1阶段：激励传播

每次迭代中的传播环节包含两步：

1. （前向传播阶段）将训练输入送入网络以获得预测结果；
2. （反向传播阶段）对预测结果同训练目标求差(损失函数)。

第2阶段：权重更新

对于每个突触上的权重，按照以下步骤进行更新：

1. 将输入激励和响应误差相乘，从而获得权重的梯度；
2. 将这个梯度乘上一个比例并取反后加到权重上。

这个比例（百分比）将会影响到训练过程的速度和效果，因此成为“训练因子”。梯度的方向指明了误差扩大的方向，因此在更新权重的时候需要对其取反，从而减小权重引起的误差。

第 1 和第 2 阶段可以反复循环迭代，直到网络对输入的响应达到满意的预定的目标范围为止。

总结

这就是神经网络的基本概念，完全基于这样的概念组成网络，称为全连接网络，可以想象，一个全连接网络中，权重变量是非常非常多的：