Transformers from Scratch
翻译自: https://e2eml.school/transformers.html
对论文Attention Is All You Need的解读。
one-hot encoding
中文叫独热编码或者一位有效编码,是指用一个N维向量表示N个词,每一个词对应一个向量,这个向量的一位为1,其余为0。
比如我们只处理三个词,那就用一个三维向量表示所有的词,并给每一个词分配一位为1:
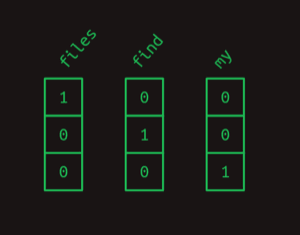
dot product (点乘)
点乘用于将两个向量相乘,即:$ \vec{p} \cdot \vec{q} $,计算方法是将两个向量对应位置的元素相乘,然后将所有结果相加。

可以很容易知道,一个one-hot vector乘自己,结果不变;一个one-hot vector乘另一个one-hot vector,结果为0。
Matrix multiplication (矩阵乘法)
一个 $ m \times n $ 的矩阵是指有m行n列的矩阵。
矩阵乘法的基础是点乘,一个只有一行的矩阵乘一个只有一列的矩阵,结果就是点乘。
一个 $ 3 \times 4 $ 的矩阵与一个 $ 4 \times 2 $ 的矩阵相乘,结果是一个 $ 3 \times 2 $ 的矩阵,计算过程如下:
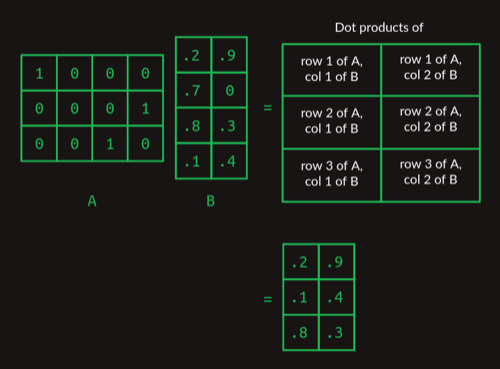
观察上图可以看出,由one-hot vector组成的矩阵与另一个矩阵相乘,其实是在选择另一个矩阵的某一行。
从计算过程可知,两个矩阵如果要能相乘,那么第一个矩阵的列数必须等于第二个矩阵的行数。
First order sequence model (一阶序列模型)
假设我们语料库里有三个句子:
- Show me my directories please. 出现次数20%
- Show me my files please. 出现次数30%
- Show me my photos please. 出现次数50%
这样我们的词汇表就是:{directories, files, me, my, photos, please, show}
可以用一个图来表示每一个单词后出现下一个单词的概率:
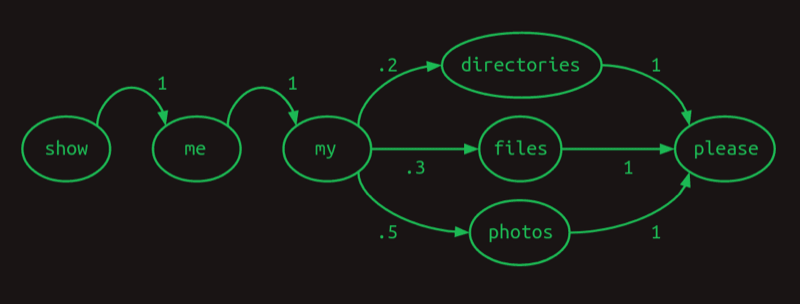
这个图叫做马尔可夫链,它表示的是一个一阶序列模型,即每一个单词出现的概率只与前一个单词有关。
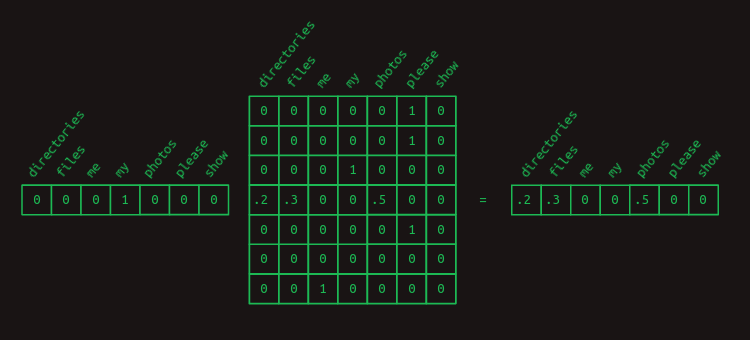
这个图可以用一个矩阵来表示,这个矩阵叫做转移矩阵,它的每一行表示一个单词,每一列表示一个单词后出现的概率,如下图所示:
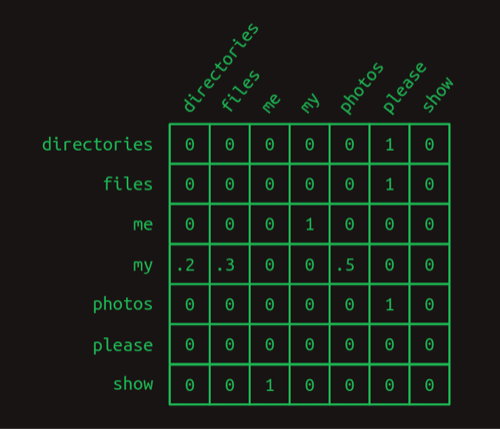
可以用矩阵乘法来计算(选择出)一个单词后出现下一个单词的概率,比如my之后出现其它单词的概率:
Second order sequence model (二阶序列模型)
假设我们语料库里有两个句子,出现概率40/60
- Check whether the battery ran down please.
- Check whether the program ran please.
如果用一阶序列模型来表示,那么ran之后出现down和please的概率是40%和60%:
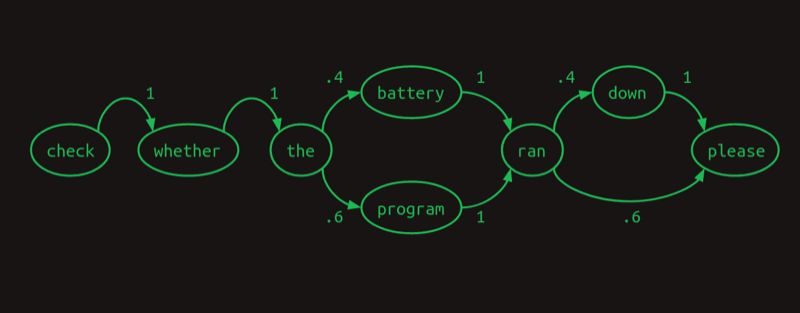
但实际上,battery ran后面出现down的概率是100%,program ran后面出现please的概率是100%。
如果用一个二阶的矩阵来表示,则是这样的:

二阶序列模型的矩阵,对于每两个单词的组合,都要占用一行,所以对于一个有N个单词的词汇表,二阶序列模型的矩阵就有$ N^2 $行。
Second order sequence model with skips (带跳跃的二阶序列模型)
如果需要向前看更远的距离,那前面的模型就会失效,比如如果向前看8个单词,就需要一个$ N^8 $行的矩阵,这样的矩阵太大了。
所以我们可以用一个带跳跃的二阶序列模型,我们看前看一个单词,同时再看每一个再之前的单词。这样我们还是看两个单词,但不再只是看之前相邻的两个。
比如这样的两个句子,出现概率50/50:
- Check the program log and find out whether it ran please.
- Check the battery log and find out whether it ran down please.
对于ran之后的词,我们除了看ran之外,还要看it, ran, weather, ran, out, ran 等等这些组合,看完之后我们发现,battery, ran可以决定后面是down,而program, ran可以决定后面是please。
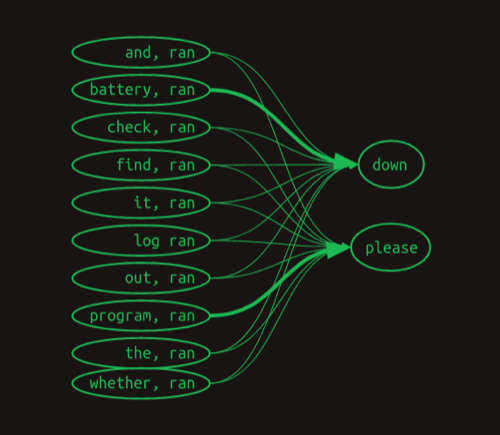
用矩阵可表示为:
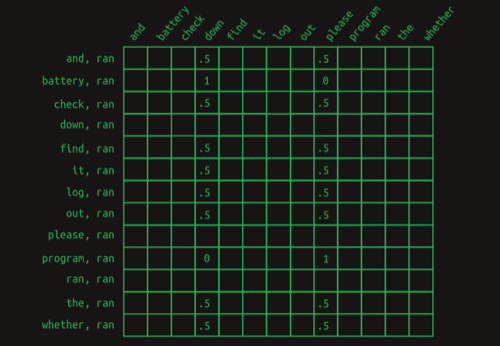
这样,当要预测ran后面词时,我们不能只看一行了,而是要看很多行(这就不再是马尔可夫链)。这里的行不再是一种状态,而是一个feature(特征)。
而表中的大部分状态都没有意义,因为它们给出后面的词的概率都是0.5。
使用这样一个表来预测下一个词,需要把所有的可能性加起来,比如对于Check the program log and find out whether it ran,对于down得到的数值为4,对于please得到的数值为5,因此我们选择please。
Masking(掩码)
在上面的例子中,4和5的区别太小了,不足以决定我们选择哪一个。可以引入mask来解决这个问题。
因为我们只看ran之前的词,而忽略ran之后的词,所以相当于我们在使用这样一个feature vector,对于ran之前的词,我们把它们的值设为1,对于ran之后的词,我们把它们的值设为0:

对于上面的例子,我们其实只关注battery, ran和program, ran,所以我们引入一个mask,只关注这两个feature:

引入mask之后,预测矩阵变为:

这时,对于之前的例子,我们就会得到down为0,please为1
这个mask,表达了对之前不同单词的不同关注程度,其实就是attention(注意力)的核心思想。
Attention as matrix multiplication (用矩阵乘法来表示attention)
可以用一个矩阵表示所有的mask,然后用one-hot vector去把想要的mask选择出来:

在论文(Attention is All You Need,以下论文都是指这篇)中,这个过程被写为 $QK^T$ :
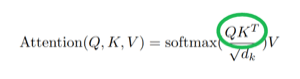
其中Q为one-hot vector,K为mask矩阵,但存储的时候是以例为mask存储的,因此需要转置。T表示转置。
Second order sequence model as matrix multiplications (用矩阵乘法来表示二阶序列模型)
下面看一下如何用矩阵乘法来生成最终的预测矩阵。
前面我们获取到了attention vector,然后用一个简单的全连接层来生成对应的单词对:
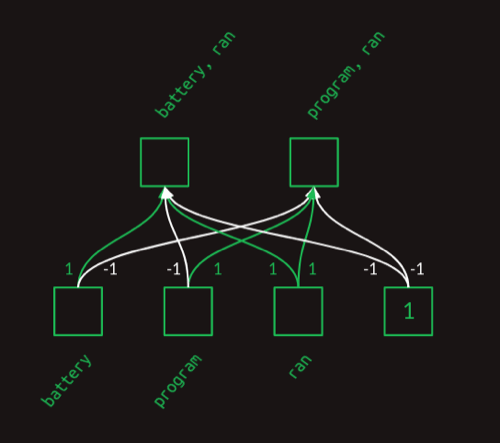
这个全连接层可以用一个矩阵来表示:
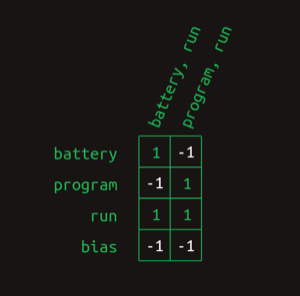
这样,用attention vector选择出单词,就是一个简单的矩阵乘法:
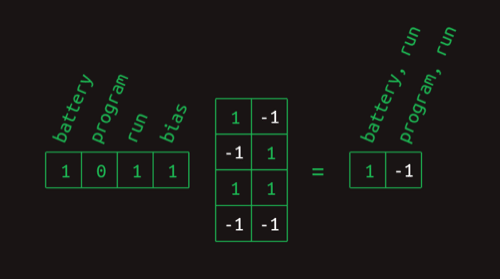
这里计算的结果有-1,我们要用一个简单的函数来把它转换为0,这个函数就是ReLU。
attention vector并不限制只能有两个1,其实也可以有多个1,这样就可以选择出多个单词。通过训练得到的attention,可以认为是学习到了人类的语言结构。
这样,获取了attention vector之后的计算就是这样三步:
- 与feature matrix相乘,计算出feature vector
- ReLU
- 与预测矩阵相乘,得到预测结果
对应论文中的:
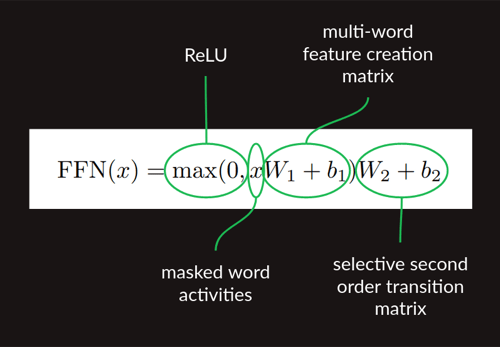
也就是架构图中的前向部分:
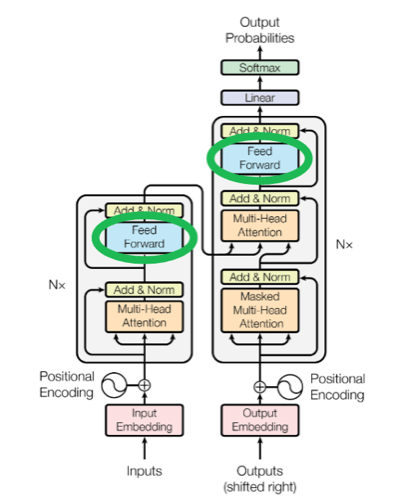
Sequence completion (序列补全)
上面的模型只能预测一个单词,如果要预测多个单词,就需要用到序列补全。
首先要给一个prompt,作为整个生成的开始。被输入到解码器中,也就是上图中右边的那一列(Outputs shifted right)
一旦解码器有了初始序列,它就进行一次前向计算。最终的结果是一组预测的单词概率分布,每个位置的序列都有一个概率分布。我们不关心序列中每个已经确定的单词的预测概率。我们真正关心的是当前序列后的下一个单词的预测概率。
有了概率后,有几种方法可以选择这个单词应该是什么,最简单的方法是greedy,选择概率最高的单词。
新的下一个单词然后被添加到序列中,在解码器底部的“输出”处替换进去,并重复这个过程。
Embeddings (嵌入)
在上面的例子中,我们使用的是one-hot vector,但是这样的方法会导致计算量过大。比如如果我们有5万个词,那最终的预测矩阵会有5万列,25亿 行。合计是125万亿个参数。这个计算量太大了。
这其实是由one-hot vector带来的问题,需要将其降维,比如对于一个小的词表,可以降到二维:
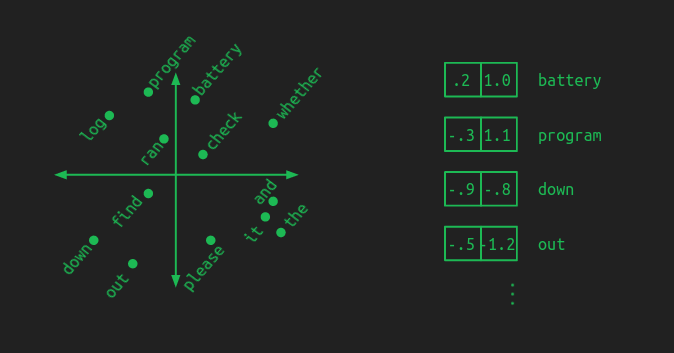
一个好的embedding,会把意思相似的词放在相近的位置,
在原论文中,embedding在架构中的位置:
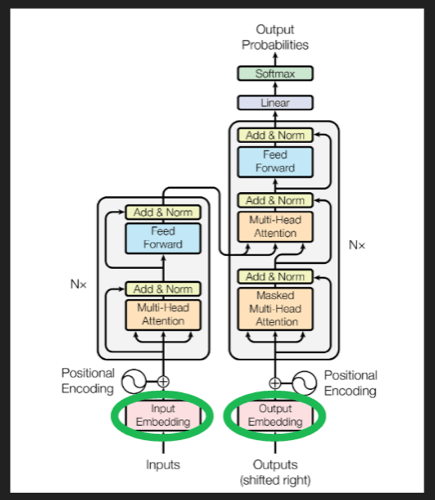
有很多非常好的计算好的embedding模型,当然也可以在训练中学习到embedding。
Positional encoding (位置编码)
之前我们只关注了单词对,并没有引入位置信息。这里使用了旋转的方式来引入位置信息:
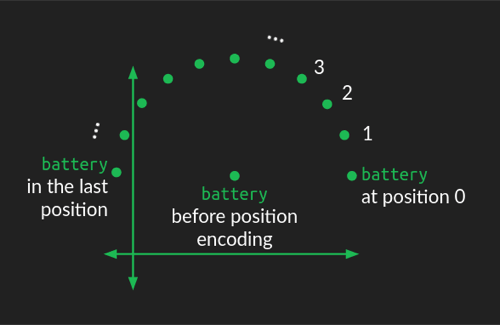
单词在embedding中的位置,作为圆心,然后根据其位置,在embedding中旋转,这样就引入了位置信息。
在原论文中,位置编码在架构中的位置:
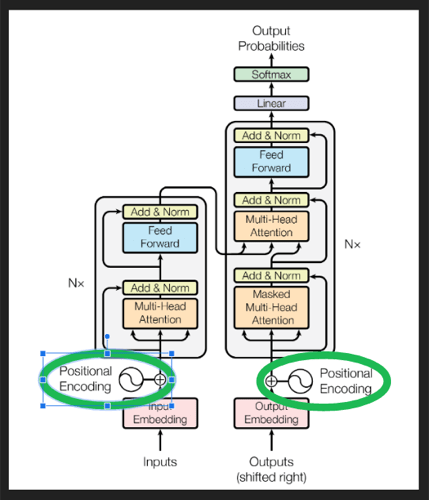
De-embeddings (解嵌入)
embedding让计算量变小,当所有的计算都完成后,需要将其解嵌入,得到one-hot vector,从而得到最终的预测结果。
Softmax
softmax函数为:$ \sigma(\vec{x}_i) = \frac{e^{x_i}}{\sum_{j=1}^{n}e^{x_j}} $
softmax的作用有:
- softmax函数可以将一个数值向量归一化为一个概率分布向量,且各个概率之和为1
- softmax函数使用了指数形式,能够将差距大的数值距离拉的更大
- softmax函数的导数形式简单,可以方便的用于反向传播
de-embedding和softmax在架构中的位置:
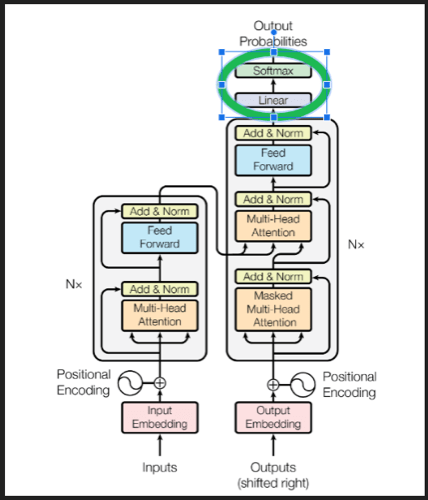
Multi-head attention (多头注意力)
在整个数据流程中,有以下一些重要的数据定义
- $N$,表示词表的大小,通常为几万个
- $n$,表示序列的长度,在GPT-3中为2048个
- $d_{model}$,表示embedding的维度,在论文中为512
这样,最初始的输入矩阵大小为 $ n \times N $,每个one-hot vector的维度为$N$,一共有$n$个单词
embedding转换矩阵的大小为 $ N \times d_{model} $
所以,将输入矩阵转换为embedding矩阵后,矩阵的大小为 $ n \times d_{model} $
Positional Encoding并不改变矩阵的大小,所以还是 $ n \times d_{model} $
attention的计算不改变矩阵大小,所以在de-embedding之前,数据还是 $ n \times d_{model} $,经过de-embedding后,数据变为 $ n \times N $,然后进入softmax,最终还是 $ n \times N $
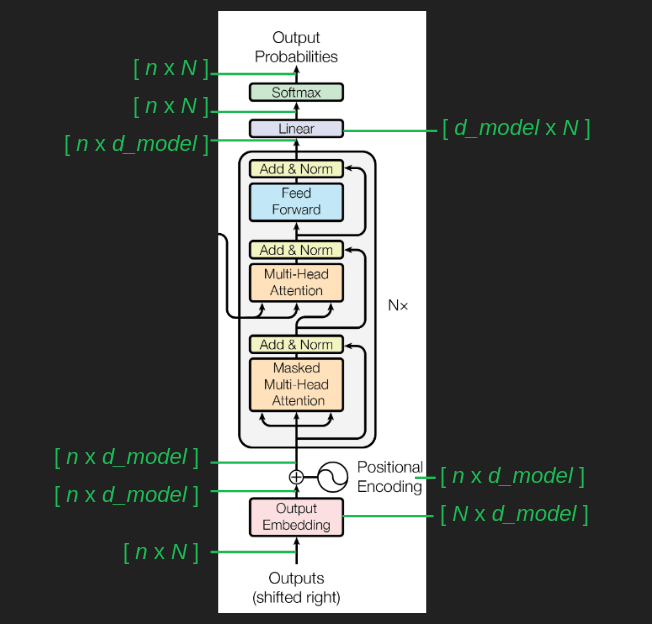
引入多头注意力
在前面提到注意力的时候,提到过,有时候注意力不仅和之前的一个词相关,也可能和多个词相关。
但是在注意力计算的时候,为了使注意力的值落在[0, 1]之间,使用了softmax,从而导致突出了最大值,丢掉了其它词的注意力值。这个问题的解 决方案就是同时计算多个注意力。
但多头注意力的同时计算,会导致计算量的增加,所以在注意力计算的时候,对embedding又做了一次变换,将其降维,在论文中使用了64维。
在计算时,有以下几个数据定义:
- $d_k$ 在论文中为64,表示用于query和key的降维后的维度
- $d_v$ 在论文中为64,表示用于value的降维后的维度
- $h$ 在论文中为8,表示多头注意力的个数
计算过程中各个数据维度的变化如下:
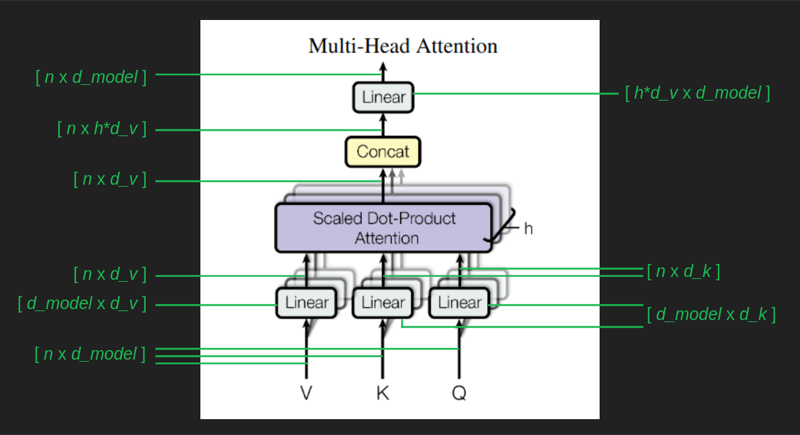
Single head attention revisited (回顾单头注意力)
由于两次高维向低维的变换,实际学习到的注意力,不是简单的单词与单词之间的关系,而是单词组之间的关系。每一个embedding点,都代表了一组单词。
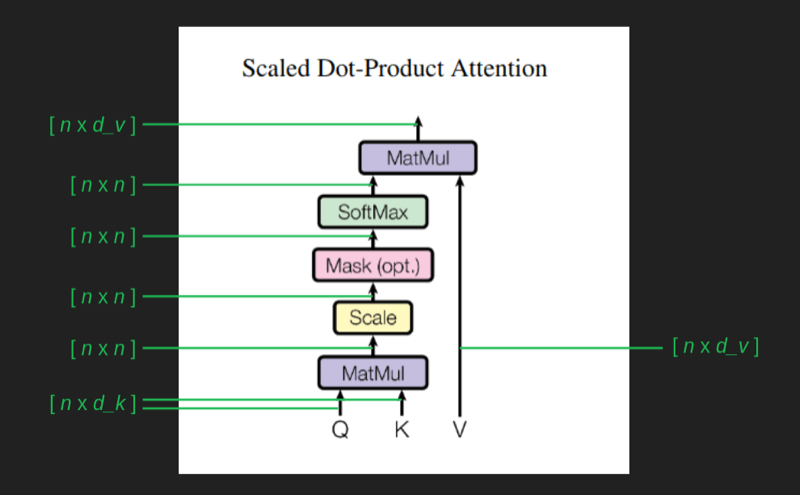
中间的mask块,确保计算的时候,只计算之间的单词,而不计算后面的单词。
Add & Norm
Skip connection (残差连接)
在计算注意力的时候,有一个残差连接,将输入的embedding和计算得到的注意力结果相加,这个架构类似于图像处理中的ResNet。
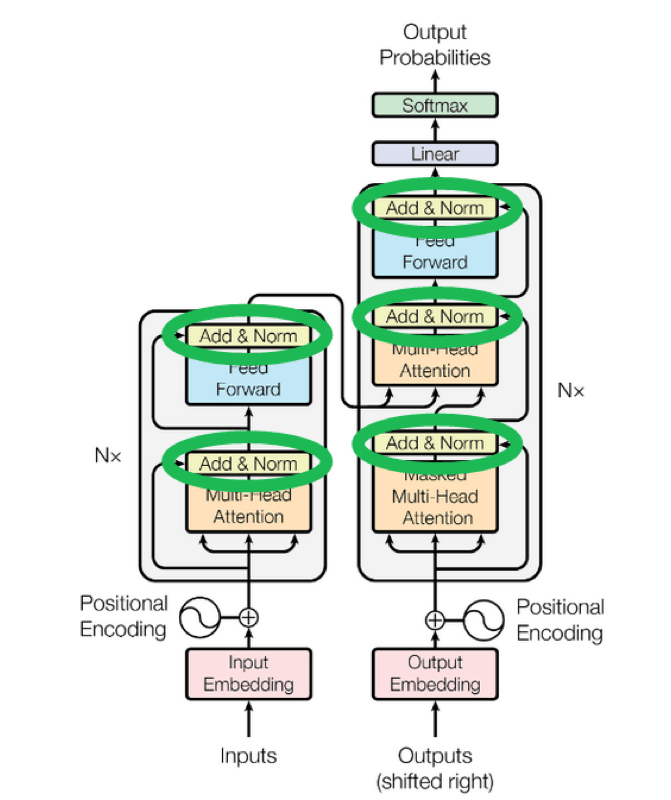
在这里,残差连接的作用有两个:
- 保证了梯度的平滑,更有利于求导(通过backpropagation进行训练)
- 保留原始的输入,避免了在attention计算中,可能会丢失最近一个单词的信息
通过残差连接,loss函数的图像可显著改善:
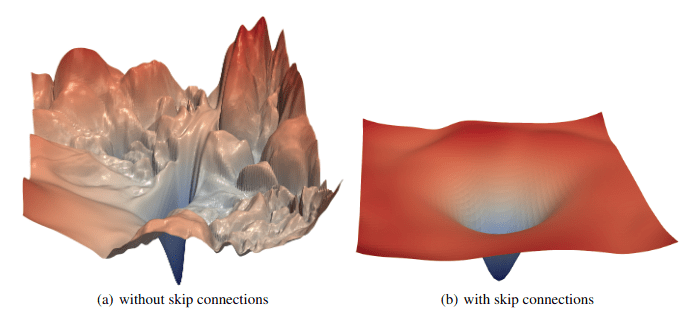
Layer normalization (层归一化)
归一化没有明确的目的,通常加在一系列计算之后,将计算之后得到的值,向平均值为0,方差为1的方向进行转换。
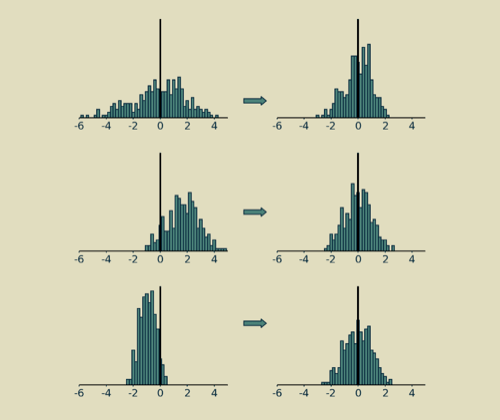
Multiple layers (多层)
在论文中,Multi-head attention和Feed Forward的过程,是重复多次的,架构图中的N(=6)表示重复的次数。
为什么需要多层,因为神经网络的训练是一个碰运气的过程,如果只有一层,只有一个最优解,那么就很难找到这个最优解,如果有多层,就有多个 最优解,就有更多的机会找到最优解(或次优解)。
Decoder stack
整个网络架构的右半部分,是decoder。有时候,只用decoder也是非常有效的,比如OpenAI的GPT,就是decoder-only的架构。
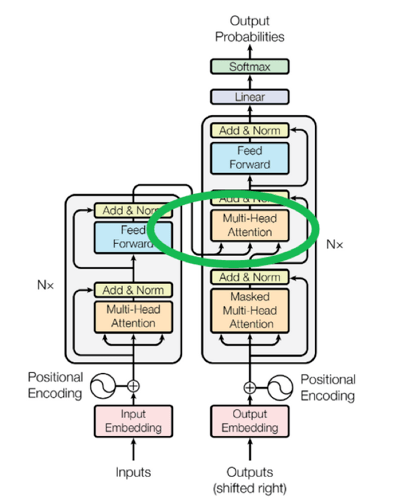
Cross-attention
cross-attention是指encoder和decoder之间的连接。这个连接将encoder的输出作为decoder的输入,这样来保留从Input来的信息。
Tokenizing
在生成开始的one-hot vector之前,我们要先确定词表的大小。一个简单的方法是直接使用一个字典,将所有的单词都放进去,但是这样的词表会非 常大,而且还有单词的各种形态变化的问题。
还有一个方法是直接使用字符作为词表,但这样的词表里包含的语义信息太少。
Byte pair encoding
解决方案是Byte pair encoding。BPE从字符开始,然后将高频的组合放入词表中,然后不断重复这个过程,一直到词表的大小达到预定的大小。