fp-ts介绍
参考 https://github.com/enricopolanski/functional-programming
基本工具
flow与pipe
先准备几个基本方法
function return1(): number {
return 1
}
function add1(x: number): number {
return x + 1;
}
function multiply2(x: number): number {
return x * 2;
}
function numberToString(x: number): String {
return `ret: ${x}`
}
flow和pipe可以用于对方法进行组合,相当于函数的compose
import { flow, pipe } from "fp-ts/function";
const func1 = flow(add1, multiply2);
pipe(1, add1, multiply2, console.log);
pipe(1, add1, multiply2, numberToString, console.log);
// 以下会报错类型错误
// console.log(pipe(1, add1, numberToString, multiply2));
console.log(func1(1))
pipe(1, func1, numberToString, console.log)
flow(return1, func1, console.log)()
Semigroup
定义Semigroup之前,先定义Magma
Magma
定义了concat函数的一个类型,就是Magma,对concat这个函数,没有任何其它要求
export interface Magma<A> {
readonly concat: (x: A, y: A) => A
}
比如:
const MagmaNumberSub: Magma<number> = {
concat: (x: number, y: number): number => x - y
}
有了concat,就可以定义一个concatAll(相当于reduce, fold)函数
export declare const concatAll: <A>(M: Magma<A>) => (startWith: A) => (as: readonly A[]) => A
将Magma限制为Semigroup
如果concat满足结合率,这样的Magma可称为Semigroup。满足了结合率的情况下,多个数据需要concat,就可以并行。比如:
a * b * c * d * e * f * g * h = ((a * b) * (c * d)) * ((e * f) * (g * h))
Semigroup的定义也是一个interface。注意这里无法在类型系统中,将结合率这个限制表达出来。
interface Semigroup<A> extends Magma<A> {}
在Semigroup下的concatAll函数,更有价值一些。
可以理解为一个Semigroup的实例,实际上是定义了对于一个数据类型进行连接、合并(输入两个值,输出一个值)的一个方式,然后就可以使用concatAll对多个值进行运算。
反向(对等)Semigroup
可以定义一个函数,自动基于一个Semigroup的实例,生成另一个反向的Semigroup:
import { Semigroup } from 'fp-ts/Semigroup'
// This is a Semigroup combinator
const reverse = <A>(S: Semigroup<A>): Semigroup<A> => ({
concat: (first, second) => S.concat(second, first)
})
自动生成乘积(结构)类型的Semigroup
import * as S from 'fp-ts/Semigroup'
import * as N from 'fp-ts/number'
type Point = {
x: number;
y: number;
}
const semigroupPoint: S.Semigroup<Point> = S.struct({
x: N.SemigroupSum,
y: N.SemigroupSum,
})
完全序(total order)数据类型的Semigroup
total order是指在一个类型中,任何两个数据都可比较大小,可排序。在这个情况下,可以有最小和最大两种Semigroup实例:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupMin: Semigroup<number> = {
concat: (first, second) => Math.min(first, second)
}
const SemigroupMax: Semigroup<number> = {
concat: (first, second) => Math.max(first, second)
}
Monoid
Semigroup再多定义一个empty,就是Monoid
import { Semigroup } from 'fp-ts/Semigroup'
interface Monoid<A> extends Semigroup<A> {
readonly empty: A
}
empty要满足两个要求:
- Right identity:
concat(a, empty) = a - Left identity:
concat(empty, a) = a
这时候如果再使用concatAll,可以不用提供初始值。
export declare const concatAll: <A>(M: Monoid<A>) => (as: readonly A[]) => A
函数式错误处理
返回错误或抛出异常的函数,不是一个完全函数(total function),是一个部分函数(partial function)。但可以通过返回一个Option类型,将这样的函数,转换为total function
Option类型可简单地定义为:
// represents a failure
interface None {
readonly _tag: 'None'
}
// represents a success
interface Some<A> {
readonly _tag: 'Some'
readonly value: A
}
type Option<A> = None | Some<A>
可以定义一个match方法,用于处理none和some的两种情况:
const match = <R, A>(onNone: () => R, onSome: (a: A) => R) => (
fa: Option<A>
): R => {
switch (fa._tag) {
case 'None':
return onNone()
case 'Some':
return onSome(fa.value)
}
}
比较两个Option类型
如果要比较两个Option类型是否相等,则要分别比较 none none; none some; some none; some some 这样四种情况
declare const o1: Option<string>
declare const o2: Option<string>
const result: boolean = pipe(
o1,
match(
() => // onNone o1
pipe(
o2,
match(
() => true, // onNone o2
() => false // onSome o2
)
),
(s1) => // onSome o1
pipe(
o2,
match(
() => false, // onNone o2
(s2) => s1 === s2 // onSome o2
)
)
)
)
fp-ts中提供了相应的函数,可生成这样的方法:
import * as E from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as O from 'fp-ts/Option'
import * as S from 'fp-ts/string'
type MyTuple = readonly [string, number]
const EqMyTuple = E.tuple<MyTuple>(S.Eq, N.Eq)
const EqOptionMyTuple = O.getEq(EqMyTuple)
const o1: O.Option<MyTuple> = O.some(['a', 1])
const o2: O.Option<MyTuple> = O.some(['a', 2])
const o3: O.Option<MyTuple> = O.some(['b', 1])
console.log(EqOptionMyTuple.equals(o1, o1)) // => true
console.log(EqOptionMyTuple.equals(o1, o2)) // => false
console.log(EqOptionMyTuple.equals(o1, o3)) // => false
Semigroup的Option类型
如果要对Option类型进行concat/concatAll,同样需要处理以上四种不同的情况。fp-ts同样提供了相应的工具,用于生成相应的函数。
import * as S from 'fp-ts/Semigroup'
import * as A from 'fp-ts/Apply'
import * as O from 'fp-ts/Option'
const semigroupSum: S.Semigroup<number> = {
concat: (x, y) => x + y,
}
const optionSemigroupSum = A.getApplySemigroup(O.Apply)(semigroupSum)
console.log(optionSemigroupSum.concat(O.some(1), O.some(2))) // some(3)
console.log(optionSemigroupSum.concat(O.some(1), O.none)) // none
console.log(S.concatAll(optionSemigroupSum)(O.some(0))([O.some(1), O.some(2)])) // some(3)
console.log(S.concatAll(optionSemigroupSum)(O.some(0))([O.some(1), O.some(2), O.none])) // none
Either类型
可以用Either取代Option用于错误处理,Either的Left,可携带错误的更多信息,而不只是一个none
引入Category Theory里的一些概念
要消除函数的副作用,有两种可能的方法:
- 定义一个DSL,将函数的副作用用数据的方式返回
- 使用thunk,将函数的副作用包装在一个可执行单元(函数)中
比如一个函数,如果要执行console.log,就是有副作用的函数:
function log(message: string): void {
console.log(message) // side effect
}
用第一种方法,是定义一个数据结构:
function log(message: string): DSL {
return {
type: "log",
message
}
}
用第二种方法,是返回一个函数:
// a thunk representing a synchronous side effect
type IO<A> = () => A
const log = (message: string): IO<void> => {
return () => console.log(message) // returns a thunk
}
所以,引入各种各样的类型,是为了对副作用进行包装:
| 类型 | 包装的副作用 |
|---|---|
ReadonlyArray<A> |
没有副作用 |
Option<A> |
可能出错的计算 |
Either<E, A> |
可能出错的计算 |
IO<A> |
不会出错的同步IO |
Task<A> |
不会出错的异步IO |
Reader<R, A> |
从环境(配置)中读取数据 |
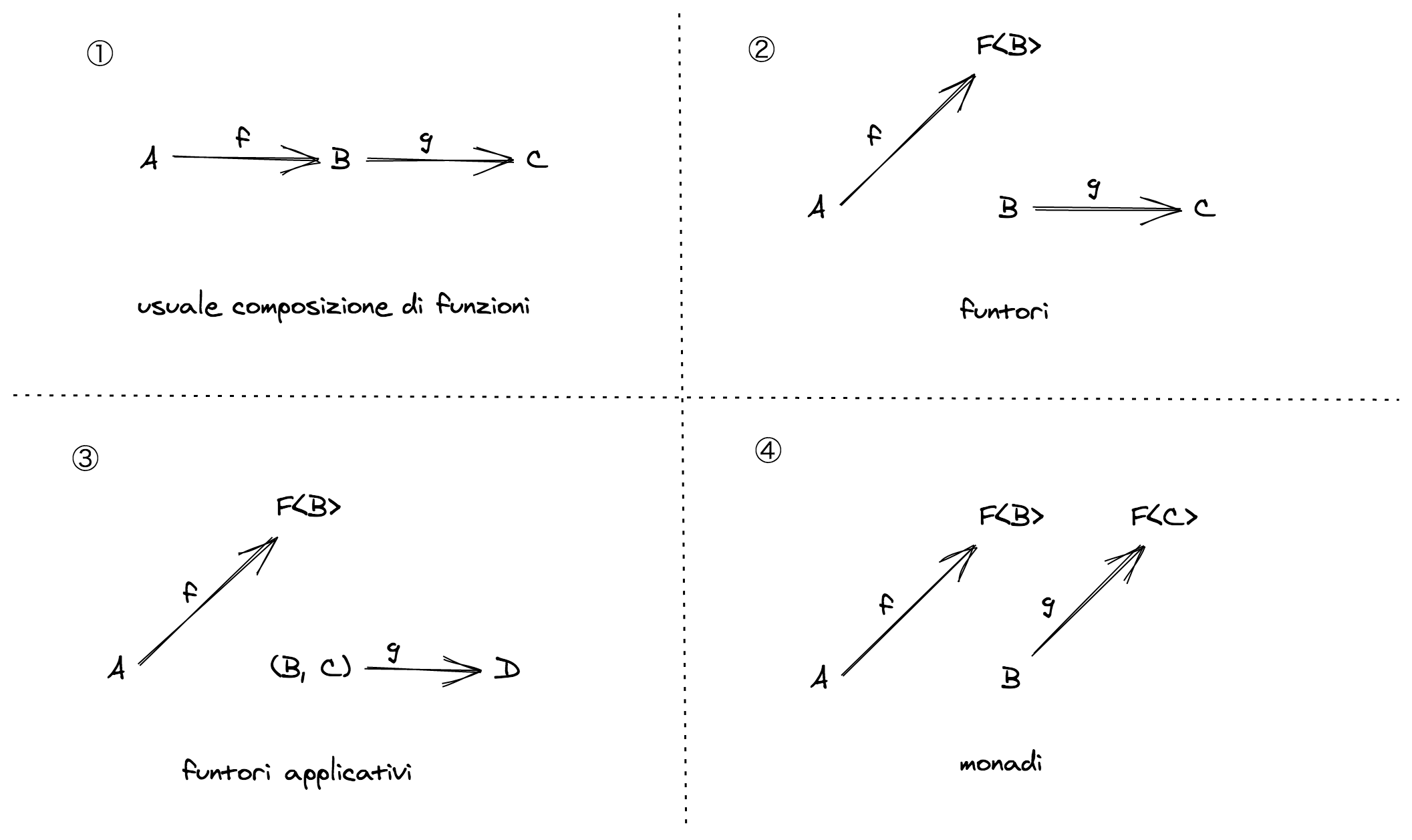
为什么需要functor, monad,是为了compose各种包含在容器中的函数,简单地说:
- 组合
f: (a: A) => B和g: (b: B) => C,需要普通的pipe/flow - 组合
f: (a: A) => F<B>和g: (b: B) => C,需要functor - 组合
f: (a: A) => F<B>和g: (b: B, c: C) => D,需要applicative functor - 组合
f: (a: A) => F<B>和g: (b: B) => F<C>,需要monad
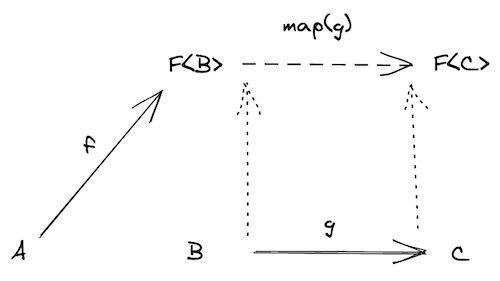
Functor
functor可以将一个 (b: B) => C的函数,转换为 (fb: F<B>) => F<C> 。
所以,如果有两个函数,一个是有副作用的 f: (a: A) => F<B>,另一个是普通纯函数 g: (b: B) => C,这两个函数不能直接组合。这时有一个F类型的map函数(functor),就可以组合了。
如果以Option为包装类,则map的例子如下:
import { flow } from 'fp-ts/function'
import { none, Option, match, some } from 'fp-ts/Option'
// transforms functions `B -> C` to functions `Option<B> -> Option<C>`
const map = <B, C>(g: (b: B) => C): ((fb: Option<B>) => Option<C>) =>
match(
() => none,
(b) => {
const c = g(b)
return some(c)
}
)
// -------------------
// usage example
// -------------------
import * as RA from 'fp-ts/ReadonlyArray'
const head: (input: ReadonlyArray<number>) => Option<number> = RA.head
const double = (n: number): number => n * 2
// getDoubleHead: ReadonlyArray<number> -> Option<number>
const getDoubleHead = flow(head, map(double))
console.log(getDoubleHead([1, 2, 3])) // => some(2)
console.log(getDoubleHead([])) // => none
Applicative Functor解决多个参数的问题
如果g函数,是 B=>C=>D,两个参数,返回一个值,这样的类型,那如何与f函数组合?如果我们有一个liftA2函数,给它一个 B=>C=>D,返回一个F<B>=>F<C>=>F<D>,那就可以解决问题
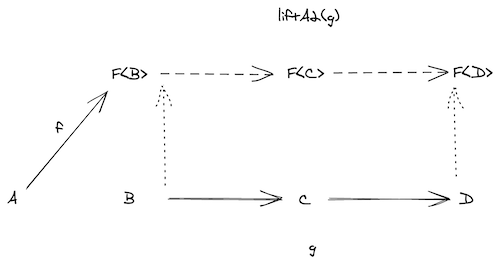
要解决这个问题,可以先用map(functor)解决第一步:
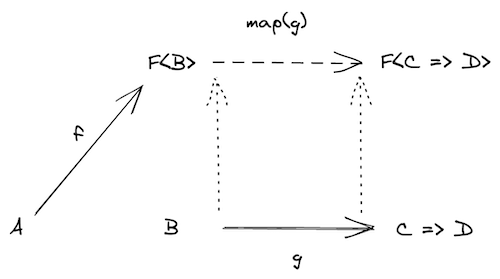
map之后有了一个F<C=>D>函数,这时候,如果能输入F<C>,返回F<D>,就能得到结果。解决方案是一个叫ap的函数。如果F是Task:
declare const ap: <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>) => Task<B>
这样就可以定义liftA2
const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D)
=> (fb: T.Task<B>) => (fc: T.Task<C>): T.Task<D>
=> pipe(fb, T.map(g), T.ap(fc))
用同样的方式,可以用ap定义出liftA3, liftA4, ……
两个类型组合ap函数
定义一个TaskOption类型,是Task中包含一个Option类型,这时的ap可以这样定义:
import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'
type TaskOption<A> = T.Task<O.Option<A>>
const of: <A>(a: A) => TaskOption<A> = flow(O.of, T.of)
const ap = <A>(fa: TaskOption<A>): (<B>(fab: TaskOption<(a: A) => B>) => TaskOption<B>) =>
flow(
T.map(<B>(gab: (O.Option<(a: A) => B>)) => (ga: O.Option<A>): O.Option<B> => O.ap(ga)(gab)),
T.ap(fa)
)
TaskOption的ap函数,要接受一个TaskOption<A>,然后接受一个TaskOption<A => B>,最后返回一个TaskOption<B>
实现:通过flow组合两个函数,返回一个: 接受Task<Option<A => B>>,返回Task<Option<B>>的函数。
- 函数1
- 先定义一个函数,接受
Option<A => B>,返回Option<A> => Option<B>- 这个函数实际上就是
Option.ap调整了参数顺序
- 这个函数实际上就是
- T.map将以上函数映射到
Task,成为:接受Task<Option<A => B>>,返回Task<Option<A> => Option<B>>
- 先定义一个函数,接受
- 函数2
- T.ap的定义是:接受一个
Task<Option<A>>,再接受一个Task<Option<A> => Option<B>>,最后返回一个Task<Option<B>> T.ap(fa)成为:接受一个Task<Option<A> => Option<B>>,返回一个Task<Option<B>>
- T.ap的定义是:接受一个
这样两个函数组合后,就成为:接受Task<Option<A => B>>,返回Task<Option<B>>
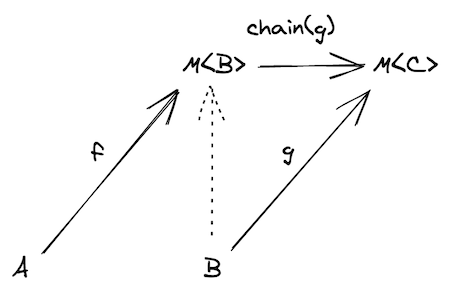
Monad解决两个有副作用的函数组合问题
如果f: (a: A) => M<B>,g: (b: B) => M<C>,如何组合?
组合的结果应该是 h: (a: A) => M<C>
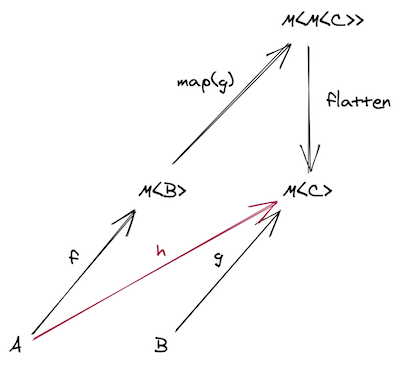
从图中可以看到,可以对g做一次map,然后将嵌套的M<M<C>>通过flatten处理回M<C>,这个先做map,再做flattern的函数,叫chain