0. 论文介绍

论文链接：link

论文中提出叫YATA(Yet Another Transformation Approach)的算法。

1. 与OT的关系

OT的本质，是对op进行集中(由服务器进行)的排序，同时对改变了顺序的op进行变换(服务器端会做，客户端也可能会做)。

op需要变换的原因与op本身的数据结构相关，因为op中记录了与位置相关的信息，改变了顺序后，原本的位置需要调整。

CRDT本质上，是分布式的排序加上一个与位置无关的数据结构。这样就不再需要服务器的排序，也不再需要在排序后对原本的操作进行变换才能应用。

2. YATA算法概述

2.1 基本前提

1. op的唯一标识。每个用户有一个自己的唯一ID userid ，同时有一个自己的操作(op)计数器。这样，每一个op就有一个由 userid 和 op counter 组成的唯一标识。
2. 数据存储。YATA将要操作的文本数据，表示为一个双向链表
3. 操作。YATA只考虑两个操作：插入和删除

2.2 插入操作

对插入操作，表示为 $ O_k(id_k, origin_k, left_k, right_k, isdeleted_k, content_k) $

• $id_k$ 是唯一标识
• $origin_k$ 是当这个操作创建时，左面的字符。此数据不可修改
• $left_k$ $right_k$ 是双向链表的两个指针，会随着内容的修改而变化
• $isdeleted_k$ 表示此字符是否被删除了
• $content_k$ 表示此次插入的内容(字符)

注意这里的 $origin_k$, $left_k$, $right_k$ 都是指向相应字符的 $id$

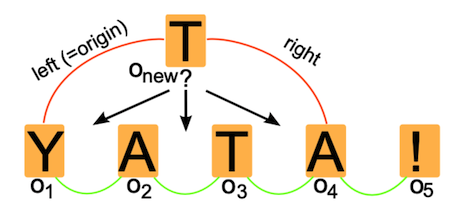
在这个图中，$O_{new}$ 为 $(id_{new}, id_{O1}, id_{O1}, id_{O4}, false, T)$ ，它想要插入到当前的序列中，这说明当创建 $O_{new}$的时候，原文还是由$O_1$和$O_4$组成的。

2.3 YATA要保证的几个原则

1. 意图保留

还是上图，算法要保证，$O_{new}$ 会插入到它自己记录的 $left_{new}$ 和 $right_{new}$ 之间。

2. 冲突插入

上图中，$O_{new}$ 与 $O_1$ $O_2$ 是冲突的，要在所有的客户端都保证一个最终一致的插入结果，就需要对操作有一个严格的排序规则。

2.4 排序规则 $<_c$

原则1. 不能交叉

对于两个冲突的操作$O_1$与$O_2$， $O_1$ 到 $origin_1$ 的连线，不能与 $O_2$ 到 $origin_2$的连线交叉。以下是两种允许的情况：

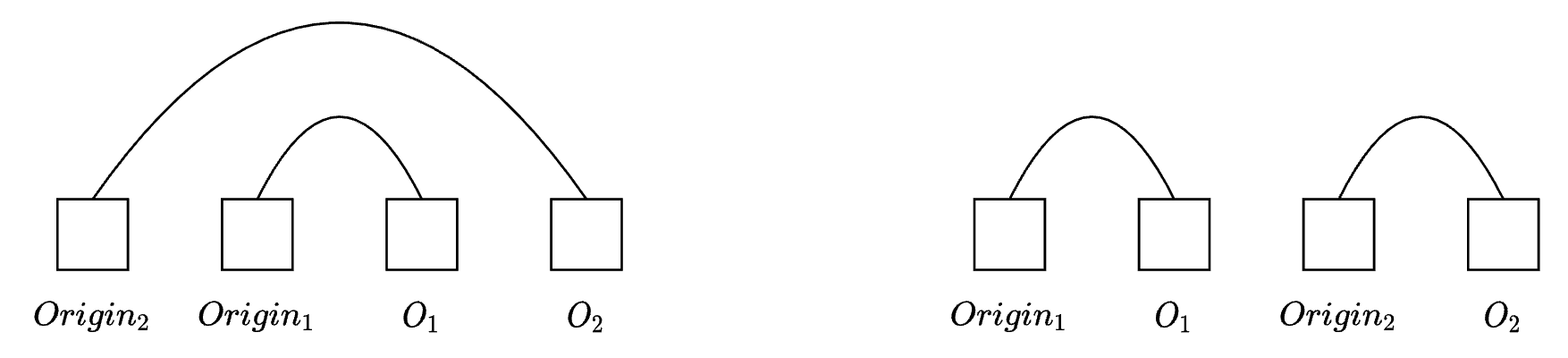
两种允许的情况分别是 包含 和 不相关

从图中可以定义 $O_1 <_{rule1} O_2$ 为：

• $origin_2 < origin_1$ 对应图中左面的包含关系
• $O_1 < origin_2$ 对应图中右面的不相关

原则2. 传递性

如果 $ O_1 <_{rule2} O_2 $，则任何满足 $ O <_{rule2} O_1 $ 的 $O$，必须同时满足 $ O <_{rule2} O_2 $

简单的说，如果O比O1小，则O不能比O2大。

原则3. userid相关

如果两个操作的origin相等，则按userid排序

满足以上三条规则，就得到了一个total order函数$<_c$，total order的含义是，对于任意两个符合定义的操作，都可以排序。

有这样的排序规则，就可以保证所有的客户端，无论以任何顺序拿到操作，最终都会得到同一个结果。

2.5 删除与垃圾回收

将一个字符标记为删除，但并不真的删除，是算法上最好的方式。这样可以保证所有的端，无论之间延时多长，都不会出问题。

在实际应用的时候，可以通过一个垃圾回收策略来做真正的删除：定时将标记为删除的操作，移动到一个buffer，再过一段时间之后，将buffer中的内容彻底清除。

3 多个客户端之间同步

每个客户端维护着自己的操作计数与其它所有端的操作计数。这样当离线后再上线的时候，可以从其它端去获取最新的操作。